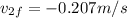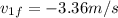Answer:
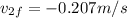
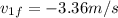
Step-by-step explanation:
As we know that system of two gliders are moving on frictionless track
so momentum conservation is applied on it
So we will have
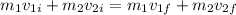
so we will have
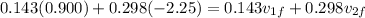
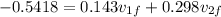
now we know that collision is elastic so we have
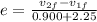
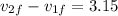
so by solving above equations we have