Question

Suppose that Jean studied for the Graduate Management Admission Test (GMAT) using a well-known preparation class and was thrilled to receive a total score of 740. Her friend Eric, however, thinks she would have scored just as well without the class. To test the efficacy of the class, they obtain a small but random sample of 17 test results from other students using the same class. This sample's average is 559.42 with a standard deviation of 108.03. In comparison, the national average was 550.12. Assume the population's results are normally distributed but that its standard deviation is not known. Jean and Eric decide to perform a two-tailed t‑test at a significance level of α = 0.05. How many degrees of freedom should they use in their calculations? df = ___.

Answer 1

Her friend Eric, however, thinks she would have scored just as well without the class, is proved at 5% significance level

Explanation:

Given that sample size is 17 and distribution is normal

Since sima, population std dev is not known, we can use only t test.

Set hypotheses as

`H_0:\bar x= 550.12\\H_a: \bar x>550.12`

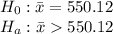
(Right tailed test)

`\bar x= 559.42\\s =108.03\\\mu = 550.12`

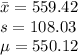
Mean difference =
`559.42-550.12=9.30`

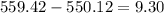
Std error of sample mean = s/square root of n

=
`(108.03)/(√(n-1) ) =27.01`

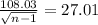
Test statistic t = mean diff/std error

= 0.3443

df = 16

p value = 0.369

Since p >0.05, at 5% significant level we conclude that there is no significant difference because of attending preparatin class.