Answer:
Mean =
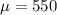
Standard deviation =
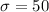
a. What percentage of adult bottlenose dolphins weigh from 400 to 600 pounds?
P(400<x<600)
Formula :

at x = 400
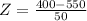
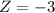
Refer the z table for p value
p value = 0.0013
at x = 600
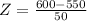

Refer the z table for p value
p value = 0.8413
P(400<x<600)=P(x<600)-P(x<400)=0.8413-0.0013=0.84
So,84% of adult bottlenose dolphins weigh from 400 to 600 pounds
b)If X represents the mean weight of a random sample of 9 adult bottlenose dolphins, what is P (500<x < 580) ?
Formula :

at x = 500
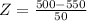
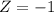
Refer the z table for p value
p value = 0.1587
at x = 580
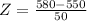

Refer the z table for p value
p value = 0.7257
P(500<x<580)=P(x<580)-P(x<500)=0.7257-0.1587=0.84
c). In a random sample of 9 adult bottlenose dolphins, what is the probability that 5 of them are heavier than 560 pounds?
at x = 560
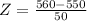
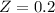
Refer the z table for p value
p value = 0.5793
P(x>560)=1-P(x<560)=1-0.5793=0.4207
Now to find the the probability that 5 of them are heavier than 560 pounds we will use binomial distribution
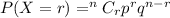
p is the probability of success that is 0.4207
q = 1-p = probability of failure
n = 9
r = 5
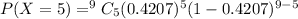
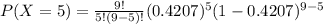
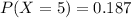
Hence In a random sample of 9 adult bottlenose dolphins, the probability that 5 of them are heavier than 560 pounds is 0.187