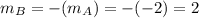Question

Help please.

The equation represents function A, and the graph represents function B.

Function A:
F(x) = -2x + 1

Function B:

Which equation best compares the slope of the two functions?

1. Slope of function B =2x slope of function A

2. Slope of function A = slope of function B

3. Slope of function A= 2x slope of function B

4. Slope of function B = -slope of function A

Answer 1

D

Explanation:

I took the test.

Answer 2

4. Slope of function B = -slope of function A

Explanation:

Given:

Function A is given as:

`F(x)=-2x+1`

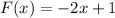
The above equation is of the form
`y=mx+b`, where
`m` represents slope of the line.

Therefore, on comparing the function A with the above standard form, er conclude that, slope of function A is -2.

Now, from the graph of function, we consider any two points on the graph and determine the slope of the line using the two points.

Let us consider the points
`(x_1,y_1)=(1.5,0)\ and\ (x_2,y_2)=(3,3)`

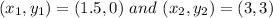
Now, the slope of the line passing through these two points is given as:

`m_B=(y_2-y_1)/(x_2-x_1)=(3-0)/(3-1.5)=(3)/(1.5)=2`

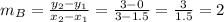
Therefore, slope of function B is 2.

Therefore, the correct relation between the slopes of the two functions is that the slope of function B is negative of the slope of function A.

`m_B=-(m_A)=-(-2)=2`