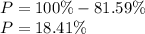Question

The average number of mosquitoes in a stagnant pond is 80 per square meter with a standard deviation of 12. If 36 square meters are chosen at random for a mosquito count, find the probability that the average of those counts is more than 81.8 mosquitoes per square meter. Assume that the variable is normally distributed.

a) 18.4%
b) 81.6%
c) 0.3%
d) 31.6%.

Answer 1

a) 18.4%

Explanation:

Assuming a normal distribution, the z-score (z) for the probability of the average of the mosquitoes count being 'X' is given by:

`z(X)=(X-\mu )/((\sigma)/(√(n)))`

Where 'μ' is the distribution mean, 'σ' is the standard deviation and 'n' is the number of square meters chosen.

For X = 81.8 and n=36:

`z(X)=(81.8 - 80)/((12)/(√(36)))\\z(X)= 0.9`

A z-score of 0.9 is equivalent to the 81.59 th percentile in a normal distribution.

Therefore, the probability (P) that the average of those counts is more than 81.8 mosquitoes per square meter is:

`P= 100\% - 81.59\%\\P=18.41\%`