Question

To solve the system of equations below, Zach isolated x in the first equation

and then substituted it into the second equation. What was the resulting
equation?
(x + y² = 25​

Answer 1

"To solve the system of equations Zach isolated x^2 into the first equation and then substituted it into the second equation.What was the resulting equation

x^2 + y^2 = 25

x^2 / 16 - y^2 / 9 = 1

Answer:

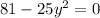`81-25 y^(2)=0` is the resulting equation

Solution:

According to question,

To solve the given system of Equations Zach isolated
`x^2` from the first equation

Given first equation is:

`x^(2)+y^(2)=25`

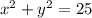
Separating
`x^2` term, we get

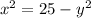`x^(2)=25-y^(2)` ------ eqn 1

And then substituted it into the second equation which is given below:-

`(x^(2))/(16)-(y^(2))/(9)=1`

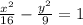
Substituting eqn 1 in above equation we get,

`(25-y^(2))/(16)-(y^(2))/(9)=1`

`9 *\left(25-y^(2)\right)-16 y^(2)=144`

`225-9 y^(2)-16 y^(2)=144`

`81-25 y^(2)=0`

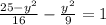
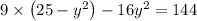
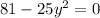
Which is the required equation