Question

One endpoint of a line segment has coordinates represented by (x+4,12y) . The midpoint of the line segment is (3,−2) .

How are the coordinates of the other endpoint expressed in terms of x and y?


(2−x,−4−12y)

(10−x,−12y)

(x+2,2−12y)

(2x−2,12y−2)

Answer 1

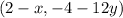`(2-x,-4-12y)` coordinates of other end points.

Explanation:

Given:

Let A be the end point whose coordinates which are given and B the other end point which co ordinates needs to be find.

Coordinates of point A
`(x_1,y_1)`=
`(x+4,12y)`

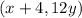
Coordinates of point A
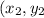`(x_2,y_2`= need to be find

Midpoint of Line segment AB = (3,-2)

Midpoint of Line segment =
`((x_1+x_2)/(2))((y_1+y_2)/(2))`

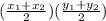
Solving for x we get ,

`(x+4+x_2)/(2)= 3\\\\x+4+x_2=6\\x_2=6-4-x\\x_2=2-x`

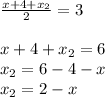
Solving for y we get ,

`(12y+y_2)/(2)= -2\\\\12y+y_2=-4\\y_2=-4-12y`

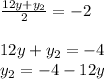
Hence
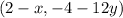`(2-x,-4-12y)` coordinates of other end points.