Question

The induced voltage on the pick-up coil with N1=20 turns is 293 mV. After adding a number of turns the new value of the induced voltage becomes 1.8 V. What is the new number of turns, N2, on the pick-up coil? Express the answer as a whole number.

Answer 1

To solve the problem it is necessary to take into account the concepts related to induced voltage.

The induced voltage, when the flow is constant, becomes directly proportional to the number of turns of the coil, that is

`\epsilon_1 = -N_1(\Phi)/(dt)`

`\epsilon_2 = -N_2(\Phi)/(dt)`

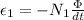
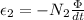
Getting the relationship we have to

`(\epsilon_1 )/(\epsilon_2) = (-N_1(Phi)/(dt))/(-N_2(Phi)/(dt))`

`(\epsilon_1 )/(\epsilon_2) = (N_1)/(N_2)`

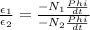
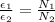
Re-arrange to find N_2 we have

`N_2 = (\epsilon_2)/(\epsilon_1)N_1`

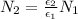
Replacing with our values

`N_2 = (1.8)/(0.293)*20`

`N_2 = 122.86\approx123 Turns`

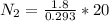
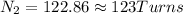
There is 123Turns at the second coil.