Question

Find the area under the curve y = tsin(t-1), x = ln(t) from x = 0 to x = ln(pi + 1)

Answer 1

The area under the curve y = tsin(t-1), x = ㏑(t) from x = 0 to x = ㏑(
`\pi` + 1) is 2 square units

Explanation:

y = tsin(t-1)

x = ㏑(t)

⇒dx =
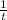`(1)/(t)`dt

x = 0 ⇒ t = 1 and x = ㏑(
`\pi`+1) ⇒ t =
`\pi`+1

Area under the curve from x = 0 to x = ㏑(
`\pi`+1) or from t = 1 to t =
`\pi`+1 is
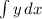`\int\limits {y} \, dx` with limits : t from 1 to
`\pi`+1

=
`\int\limits {tsin(t-1)} \, (1)/(t) dt`

=
`\int\limit {sin(t-1)} \, dt`

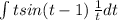
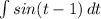
Using the substitution t = k + 1 :

dt = dk

when t = 1, k = 0 and when t =
`\pi`+1, k =
`\pi`

The integral is now modified as :

`\int\limits^\pi _0 {sin(k)} \, dk`

= -(cos(
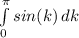
`\pi`)-cos(0))

= -(-1-1)

= -(-2)

= 2 square units.