Question

The town of Hayward (CA) has about 50,000 registered voters. A political research firm takes a simple random sample of 500 of these voters. In the sample, the breakdown by party affiliation is 115 Republicans, 331 Democrats, and 54 Independents. Calculate a 98% confidence interval for the true percentage of Independents among Haywards 50,000 registered vote.

Answer 1

(0.0757;0.1403)

Explanation:

1) Data given and notation

Republicans =115

Democrats=331

Independents=54

Total= n= 115+331+54=500

`\hat p_(ind)=(54)/(500)=0.108`

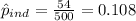
Confidence=0.98=98%

2) Formula to use

The population proportion have the following distribution

`\hat p \sim N(p,\sqrt{(p(1-p))/(n)})`

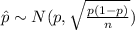
The confidence interval for the population proportion is given by this formula

`\hat p \pm z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}`

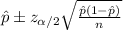
We have the proportion of independents calculated

`\hat p_(ind)=(54)/(500)=0.108`

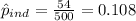
We can calculate
`\alpha=1-conf=1-0.98=0.02`

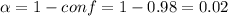
And we can find
`\alpha/2 =0.02/2=0.01`, with this value we can find the critical value
`z_(\alpha/2)` using the normal distribution table, excel or a calculator.

On this case
`z_(\alpha/2)=2.326`

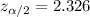
3) Calculating the interval

And now we can calculate the interval:

`0.108 - 2.326\sqrt{(0.108(1-0.108))/(500)}=0.0757`

`0.108 + 2.326\sqrt{(0.108(1-0.108))/(500)}=0.1403`

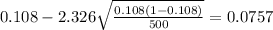
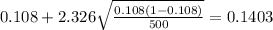
So the 98% confidence interval for this case would be:

(0.0757;0.1403)