Question

Given the following exponential function, identify whether the change represents

growth or decay, and determine the percentage rate of increase or decrease.
y = 91(0.938)^x

Answer 1

The change represents the decay

The percentage rate of decrease is 6.2%

Explanation:

The formula of the exponential growth is y = a
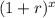`(1+r)^(x)` , where

• a is the initial value

• r is the rate of increase in decimal ⇒ (1 + r) > 1

The formula of the exponential decay is y = a
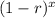`(1-r)^(x)` , where

• a is the initial value

• r is the rate of decrease in decimal ⇒ (1 - r) < 1

Let us solve the question.

∵ y = 91
`(0.938)^(x)`

→ Compare it with the forms above

∴ a = 91

∵ The rate of change is 0.938

∵ 0.938 < 1

→ That means the rate of change is decreasing

∴ The function y = 91
`(0.938)^(x)` represents exponential decay

∴ The change represents the decay

→ From the 2nd form above

∵ (1 - r ) = 0.938

→ Subtract 1 from both sides

∴ 1 - 1 - r = 0.938 - 1

∴ - r = - 0.062

→ Divide both sides by -1

∴ r = 0.062

→ Multiply it by 100% to change it to a percentage

∵ 0.062 × 100% = 6.2%

∴ r = 6.2%

∴ The percentage of decrease is 6.2%