Question

The number of winter storms in a good year is a Poisson random variable with mean 3, whereas the number in a bad year is a Poisson random variable with mean 5. If next year will be a good year with probability .4 or a bad year with probability .6, find the expected value and variance of the number of storms that will occur.

Answer 1

Answer: Mean = 4.8 and variance = 5.16

Explanation:

Since we have given

Let X be the number of storms occur in next year

Y= 1 if the next year is good.

Y=2 if the next year is bad.

Mean for good year = 3

probability for good year = 0.4

Mean for bad year = 5

probability for bad year = 0.6

So, Expected value would be

`E[x]=\sum xp(x)\\\\=3* 0.4+5* 0.6\\\\=1.2+3\\=4.2`

Variance of the number of storms that will occur.

`Var[x]=E[x^2]-(E[x])^2`

`E[x^2]=E[x^2|Y=1].P(Y=1)+E[x^2|Y=2].P(Y=2)\\\\=(3+9)* 0.4+(5+25)* 0.6\\\\=12* 0.4+30* 0.6\\\\=4.8+18\\\\=22.8`

So, Variance would be

`\sigma^2=22.8-(4.2)^2\\\\=5.16`

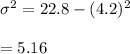
Hence, Mean = 4.8 and variance = 5.16