Question

The river is 500 miles long. It took the canoe group 5 hours to travel down river and 10 hours to paddle back up river. How fast were they paddling? How fast was the current?

Answer 1

Boat speed = 75 miles/ h

Current speed = 25 miles/ h

Explanation:

Remember that:

`s = (d)/(t)`

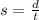
Where

s is the speed

d is the distance

t is the time.

If we call s the speed of the boat and we call c the speed of the current, then we have to:

Boat speed downstream (Boat speed in the same direction as river speed):

`(s + c) = (d)/(t_1)`

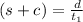
Where:

`d = 500\ miles`

`t_1 = 5\ h`

`s + c = (500)/(5)\\\\s + c = 100`

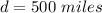
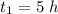
Boat speed upstream (Boat speed in the opposite direction than the river speed):

`(s-c) = (d)/(t_2)`

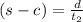
Where:

`d = 500\ miles`

`t_2 = 10\ h\\\\s-c = (500)/(10)\\\\s-c = 50`

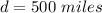
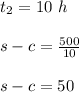
Then we have the following system of equations:

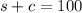`s + c = 100` (1)

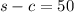`s-c = 50` (2)

Add equation (1) with equation (2) and solve for s:

`2s = 150\\\\s = 75`

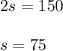
Now substitute s in equation (2) and solve for c

`75 - c = 50\\\\c = 75-50\\\\c = 25`

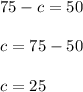
Finally

Boat speed = 75 miles/ h

River speed = 25 miles/ h