Question

Water is leaking out of an inverted conical tank at a rate of at the same time that water is being pumped into the tank at a constant rate. The tank has height m and the diameter at the top is m. If the water level is rising at a rate of when the height of the water is m, find the rate at which water is being pumped into the tank.

Answer 1

Water is leaking out of an inverted conical tank at a rate of 10,500 cm3/min at the same time that water is being pumped into the tank at a constant rate. The tank has height 6 m and the diameter at the top is 4 m. If the water level is rising at a rate of 20 cm/min when the height of the water is 2 m, find the rate at which water is being pumped into the tank

Answer:

The rate at which water is being pumped into the tank is 289,752
`cm^3/min`

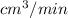
Solution:

According to question,

There is an inverted conical tank, through which water is leaking at a rate of 10,500 cm3/min at the same time that water is being pumped into the tank at a constant rate

The dimension of tank are:

Diameter = 4cm

Radius(r) =
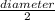`(diameter)/(2)` = 2cm

Height = 6cm

Clearly we can see that height is 3 times radius so, we can write

h = 3r OR r = h/3 ……………………. (1)

The volume of cone "V" is given as:

`\text { volume of cone }(\mathrm{V})=(1)/(3) \pi r^(2) h` -------- (2)

From (1) and (2)

`\text { Volume of cone(V) }=(1)/(3) \pi\left((h)/(3)\right)^(2) h`

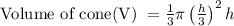
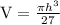`\mathrm{V}=(\pi h^(3))/(27)` -------- (3)

Now we calculate the derivate:-

`(d V)/(d t)=(3 \pi h^(2))/(27) (d h)/(d t)`

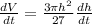
`(d V)/(d t)=(\pi h^(2))/(9) (d h)/(d t)` --------- (4)

According to question, when height is 2m = 200cm, the water level is rising at a rate of 20 cm/min

`(d h)/(d t)=20 \mathrm{cm} / \mathrm{min}`

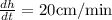
On putting above values in equation(4) and solving we get

`(d V)/(d t)=279252`

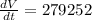
Hence, the rate at which water is being pumped is 289,752
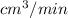`cm^3/min` which is the sum of water volume increasing at rate of 279,252 and 10,500 leaking out