Question

walnut grower estimates from past records that if 20 trees are planted per acre, then each tree will average 60 pounds of nuts per year. If, for each additional tree planted per acre, the average yield per tree drops 2 pounds, then how many trees should be planted to maximize the yield per acre? What is the maximum yield?

Answer 1

5 trees should be planted to maximize the yield per acre,

The maximum yield would be 1250

Explanation:

Given,

The original number of trees per acre = 20,

Average pounds of nuts by a tree = 60,

Let x be the times of increment in number of trees,

So, the new number of trees planted per acre = 20 + x

∵ for each additional tree planted per acre, the average yield per tree drops 2 pounds,

So, the new number of pounds of nut = (60 - 2x)

Thus, the total yield per acre,

`Y(x) = (20+x)(60-2x)`

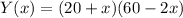
Differentiating with respect to t ( time ),

`Y'(x) = (20+x)(-2) + 60 - 2x = -40 - 2x + 60 - 2x = 20 - 4x`

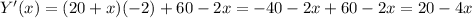
Again differentiating with respect to t,

`Y''(x) = -4`

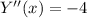
For maxima or minima,

`Y'(x) = 0`

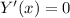
⇒ 20 - 4x = 0

⇒ 20 = 4x

⇒ x = 5,

For x = 5, Y''(x) = negative,

Hence, Y(x) is maximum for x = 5,

And, maximum value of Y(x) = (20+5)(60 - 10) = 25(50) = 1250,

i.e. 5 trees should be planted to maximize the yield per acre,

and the maximum yield would be 1250 pounds