Question

Hey Everyone, I really need help on this asap, thank you so much :)

Answer 1

The size of the angle is 60°.

Explanation:

Let name the regular hexagon as ABCDEF and the Rhombus as ABOF.

Let angle AFO and angle ABO be y (opposite angles of a rhombus are equal)

To Find :

`\angle OBC = x = ?`

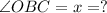
Solution:

As we know polygon ABCDEF is a regular hexagon then we have

`\textrm{some of all the interior angles} = 720\\ \angle A + \angle B + \angle C + \angle D + \angle E + \angle F = 720\\`

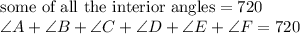
As it is a regular hexagon all angles are equal

∴
`\angle A + \angle A + \angle A + \angle A + \angle A + \angle A = 720\\`

`6\angle A = 720\\\angle A = 120\\`

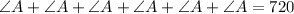
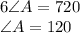
i.e
`\angle B = 120\\\angle F = 120`

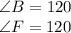
Now quadrilateral ABOF is a rhombus given.

Therefore. Opposite angles of rhombus are equal.

∴
`\angle A = \angle BOF = 120\\and\\\angle AFO = \angle ABO = y (say)`

Now in a quadrilateral sum of all the angles is 360°

∴
`\angle A + \angle BOF + \angle AFO + \angle ABO = 360\\120 + 120 + y + y = 360\\2y = 120\\y = 60`

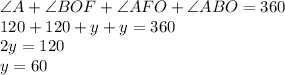
But

`\angle B = \angle ABF + \angle OBC\\120 = y + x\\120 = 60 + x\\x = 60`

Therefore the size of angle x is 60°