Question

We toss three fair coins simultaneously and independently. If the outcomes of all coin tosses are the same, we win; otherwise, we lose. Let A be the event that the first coin and second coin come up heads, B be the event that the second coin and third coin come up heads, and C be the event that we win. Determine whether the below events are true or false.

A. Events A and B are not independent.
B. Events A and C are independent.
C. Events A and B are conditionally independent given C.
D. Events A and C are conditionally independent given B.
E. The probability of winning is 3

Answer 1

A. TRUE B. FALSE C. FALSE D. FALSE E. FALSE

Explanation:

The sample space is S = {HHH, HHT, HTH, THH, TTT, TTH, THT, HTT}, and we have the following events.

A = {HHH, HHT}

B = {THH, HHH}

C = {HHH, TTT}

A. P(A\cap B) = P({HHH}) = 1/8, P(A) = 1/4, P(B) = 1/4, P(A)P(B) = (1/4)(1/4) = 1/16. Because
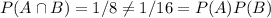`P(A\cap B) = 1/8 \\eq 1/16 = P(A)P(B)`, we have that A and B are not independent.

B. P(A\cap C) = P({HHH}) = 1/8, P(A) = 1/4, P(C) = 1/4, P(A)P(C) = (1/4)(1/4) = 1/16. Because
`P(A\cap C) = 1/8 \\eq 1/16 = P(A)P(C)`, we have that A and C are not independent.

C. Given C = {HHH, TTT}, A = {HHH}, B = {HHH},
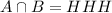`A\cap B = {HHH}`, i.e., P(A|C)=1/2, P(B|C)=1/2 and
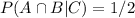`P(A\cap B|C)=1/2`. Because
`P(A\cap B|C) = 1/2\\eq (1/2)(1/2) = P(A|C)P(B|C)` events A and B are not conditionally independent given C.

D. Given B = {THH, HHH}, A = {HHH}, C={HHH},
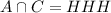`A\cap C = {HHH}`, i.e., P(A|B)=1/2, P(C|B)=1/2 and
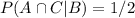`P(A\cap C|B)=1/2`. Because
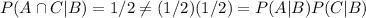`P(A\cap C|B) = 1/2\\eq (1/2)(1/2) = P(A|B)P(C|B)` events A and C are not conditionally independent given B.

E. The probability of winning is P(C) = 2/8 = 1/4