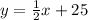The required equation is
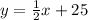
Solution:
Given that , you go to MetroPCS and can talk for 60 minutes with the plan for $55, and 90 minutes with a plan that cost $70.
We have to write an equation in slope intercept form that represents the total cost Y of talking for X number of minutes with MetroPCS plan.
We know that, slope intercept form of equation is y = mx + c
Where "m" is the slope of line and "c" is the y-intercept
Now, for 1st case, 60 minutes ⇒ $55
Substitute these values in our equation 55 = 60m + c ⇒ (1)
And for 2nd case 90 minutes ⇒ $70
By substituting those values in equation, 70 = 90m + c ⇒ (2)
Now, subtract (1) from (2)
90m + c = 70
60m + c = 55
(-)---------------
30m + 0 = 15
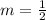
Then from eqn 1,
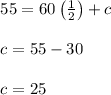
Then our equation is modified as