Question

the eccentricity of a hyperbola is defined as e=c/a. find an equation with vertices (1,-3) and (-3,-3) and e=5/2

Answer 1

`((x + 1 )^(2) )/(4) - ((y + 3 )^(2) )/(21) = 1`.

Explanation:

If (α, β) are the coordinates of the center of the hyperbola, then its equation of the hyperbola is
`((x - \alpha )^(2) )/(a^(2) ) - ((y - \beta )^(2) )/(b^(2) ) = 1`.

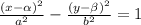Now, the vertices of the hyperbola are given by (α ± a, β) ≡ (1,-3) and (-3,-3)

Hence, β = - 3 and α + a = 1 and α - a = -3

Now, solving those two equations of α and a we get,

2α = - 2, ⇒ α = -1 and

a = 1 - α = 2.

Now, eccentricity of the hyperbola is given by
`b^(2) = a^(2)(e^(2)  - 1) = 4[((5)/(2) )^(2) -1] = 21` {Since
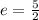`e = (5)/(2)` given}

Therefore, the equation of the given hyperbola will be

`((x + 1 )^(2) )/(4) - ((y + 3 )^(2) )/(21) = 1`. (Answer)