Question

A 100 g ball on a 55-cm-long string is swung in a vertical circle about a point 200 cm above the floor. The string suddenly breaks when it is parallel to the ground and the ball is moving upward. The ball reaches a height 600 cm above the floor.What was the tension in the string an instant before it broke?Express your answer to two significant figures and include the appropriate units.

Answer 1

T=14.27N

Step-by-step explanation:

The very first thing we need to do in order to solve this problem is do a drawing of the situation so we can visualize it better. (See attached picture).

So next, as we can see in the free body diagram, there are two forces, one acting in the horizontal direction and the other acting in the vertical direction. At this point we only care about the horizontal force, which is the force of tension. Before the string broke, the ball had an acceleration directed towards the center of the circle. This is the centripetal acceleration provided by the tension of the string. So we can now do a sum of forces:

`\sum F=ma_(c)`

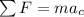
since there is only one force, then our equation turns to:

`T=ma_(c)`

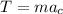
we know what the mass of the ball is, but we don't know what the centripetal acceleration is. We can figure that out though by analyzing the second stage of the problem. When the string breaks, the ball will be directed upwards with a given velocity, we can determine what this velocity is by either using kinematic formulas or by doing some energy balance. I'll solve this by using kinetic and potential energies.

So on the begining, let's call this point A, the ball had two types of energy, Kinetic and Potential. In the highest point, the ball will only have potential energy, since its velocity is zero at that point, so our equation is then:

`U_(A)+K_(A)=U_(B)`

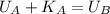
So now we can rewrite the equation like this:

`mgh_(A)+(1)/(2)mV_(A)^(2)=mgh_(B)`

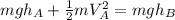
which can be simplified by dividing both sides of the equation by the mass, so we get:

`gh_(A)+(1)/(2)V_(A)^(2)=gh_(B)`

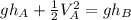
So now we can solve this equation for the Velocity in point A:

`(1)/(2)V_(A)^(2)=gh_(B)-gh_(A)`

`V_(A)^(2)=2g(h_(B)-h_(A))`

`V_(A)=\sqrt{2g(h_(B)-h_(A))}`

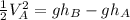
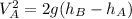
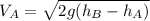
and now we can substitute the values provided by the problem:

`V_(A)=\sqrt{2(9.81m/s^(2))(600x10^(-2)m-200x10^(-2)m)}`

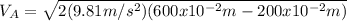
which yields:

`V_(A)=8.86m/s`

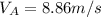
Now we know how fast was the ball moving when the string broke, so we can use that to find the centripetal acceleration:

`a_(c)=(V^(2))/(r)`

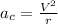
so we get:

`a_(c)=((8.86m/s)^(2))/(55x10^(-2)m)`

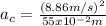
which yields:

`a_(c)=142.73m/s^(2)`

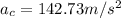
so now we can us this to find the tension of the string at that time:

`T=ma_(c)`

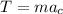
so we get:

`T=(100x10^(-3)kg)(142.73m/s^(2))`

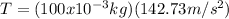
so

T=14.27N