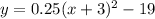Question

Equation of parabola in vertex form that had vertex at -3,-19 and pass through 5,-3

Answer 1

The standard parabolic equation is

`y = 0.25(x  +3)^2 -19`

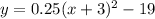
Explanation:

Here, the vertex of parabola is (h,k) = ( -3,-19)

The points on the given parabola is ( 5,-3)

Now, the general form of the Parabolic Equation is
`y = a(x - h)^2 + k`

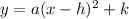
(1) Substitute Coordinates (h,k) for the Vertex

`y = a(x - h)^2 + k \implies y = a ( x - (-3)) ^2 + (-19)\\or, y = a( x+3)^2 - 19`

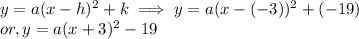
(2)Substitute point Coordinates (x,y)

`y = a( x+3)^2 - 19  \implies-3 = a(5+3)^2 -19\\or, -3 = 64 a -19\\\implies 64 a = 16\\or, a = 16/64 = 0.25`

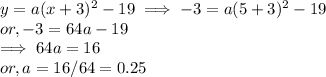
⇒ a =0.25

Substituting the values of (h,k) and a in the standard for, we get,

The standard parabolic equation is
`y = 0.25(x  +3)^2 -19`