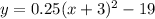Answer:
The standard parabolic equation is
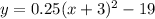
Explanation:
Here, the vertex of parabola is (h,k) = ( -3,-19)
The points on the given parabola is ( 5,-3)
Now, the general form of the Parabolic Equation is
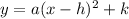
(1) Substitute Coordinates (h,k) for the Vertex
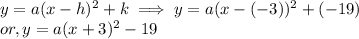
(2)Substitute point Coordinates (x,y)
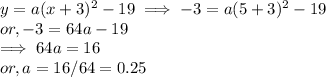
⇒ a =0.25
Substituting the values of (h,k) and a in the standard for, we get,
The standard parabolic equation is