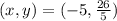Question

Find the point that is 1/5 the way from A to B where
A(-7,4) and B(3, 10).

Answer 1

The coordinates of the point that is 1/5 the way from A to B is
`(x,y) = (-5,(26)/(5))`

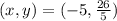
Explanation:

Here, the given points are: A (-7,4) and B (3,10)

Let us assume the point M(x,y) on AB is such that

AM : AB = 1 : 5

⇒ AM : (AB - AM) = 1 : (5-1) = 1: 4

⇒ AM : MB = 1 : 4

Now, The Section Formula states the coordinates of point (x,y) on any line dividing the line in the ratio m1 : m2

`(x,y) = ((m_2x_1+m_1x_2)/(m_1+m_2) ,(m_2y_1+m_1y_2)/(m_1+m_2)  )`

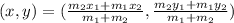
Here, in the given equation, m1: m2 = 1:4

So, the coordinates M(x,y) is given as:

`(x,y) = (((-7)(4) + 1 (3))/(1+ 4) ,(4(4) + 1(10))/(1+4)  )\\\implies (x,y) = ((-28+3)/(5) ,(16+10)/(5) )  = ((-25)/(5) ,(26)/(5) )\\\implies (x,y) = (-5,(26)/(5) )`

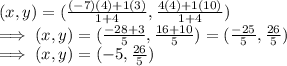
Hence, the coordinates of the point that is 1/5 the way

from A to B is
`(x,y) = (-5,(26)/(5))`