Question

Suppose the mass of a basilisk lizard is 90.0 g, the mass of each foot is 3.00 g, the speed of a foot as it slaps the water is 1.50 m/s, and the time for a single step is 0.600 s. (a) What is the magnitude of the impulse on the lizard during the slap? (Assume this impulse is directly upward.) (b) During the 0.600 s duration of a step, what is the downward impulse on the lizard due to the gravitational force? (c) Which action, the slap or the push, provides the primary support for the lizard, or are they approximately equal in their support?

Answer 1

a) I =0.0045 Ns

b) I= 005292 Ns

c) Push

Step-by-step explanation:

1) Data given and useful definition

`m_(lizard)=90gr`

`m_(foot)=3gr`

`v_f =0(m)/(s)`

`v_i =1.5(m)/(s)`

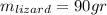
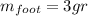
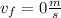
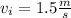
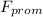`F_(prom)` is the average force

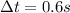`\Delta t=0.6s` represent the duration steps

Impulse is defined as: "The change of momentum of an object when the object is acted upon by a force for an interval of time"

2) Part a

We can calculate the impulse during the slap with this formula:

`I=\Delta p=m_(foot)(v_f -v_i)`

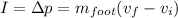
And replacing we got:

`I=\Delta p=0.003kg(0 -1.5)(m)/(s)=-0.0045Ns`

but on this case is moving on positive direction so then I=0.0045Ns

3) Part b

The impulse for this case would be given by:

`I=F_(prom)\Delta t`

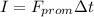
Since the downward impulse on the lizard due to the gravitational force that represent that the average force would be the graviational force, and replacing we have:

`I=m_(lizard)g\Delta t`

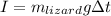
And replacing the values we got:

`I=0.09Kg 9.8(m)/(s^2) 0.6s=0.5292Ns`

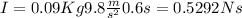
4) Part c

Based on the values obtained for parts a) and b) we see that the impulse for the slapping is very low to surpass the impulse due to the gravitational force. So on this case needs to be push to provides the primary support for the lizard.