Option A
The line
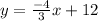 is perpendicular to
is perpendicular to
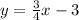
Solution:
Given that line is
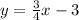
We have to find the line perpendicular to this line.
The given line equation is in form of slope-intercept form
The slope-intercept form is given as:
y = mx + c
Where "m" is the slope of the line and "c" is the y-intercept
On comparing the given equation with slope-intercept form, we get
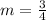
If a line is perpendicular to another line, then the product of their slopes will always be -1
Let the slope of line which is perpendicular to given line be "a"
Then we get,
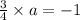
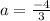
Now look at the options and compare with slope intercept form and find out which option has the slope "m" =
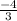
Option A
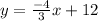 has the slope
has the slope
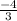
Thus option A is correct