Question

How many terms are in the geometric series 8+40+200+...+3,125,000

Answer 1

There are 9 terms in geometric series 8 + 40 + 200 + ... + 3,125,000

Solution:

Need to determine how nay terms are there in following geometric series

8 + 40 + 200 + ... + 3,125,000

Let’s derived basic properties of given geometric series which will be helpful in evaluating number of terms

`\begin{array}{l}{\text { First term of given geometric series is } a_(1)=8} \\\\ {\text { Second term of given geometric series is } a_(2)=40} \\\\ {\text { Third term of given geometric series is } a_(3)=200}\end{array}`

`\text { Common ratio of geometric series } \mathrm{r}=(a_(2))/(a_(1))=(a_(3))/(a_(2))=5`

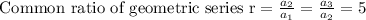
Formula for nth term of geometric series is as follows

`a_(n)=a_(1) r^((n-1))`

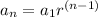
As last term is 3,125,000

`\text { So } a_(n)=3,125,000`

On substituting value of
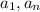`a_1, a_n` and r is formula of nth term of geometric series we get

`\begin{array}{l}{3,125,000=8 * 5^((n-1))} \\\\ {=>(3125000)/(8)=5^((n-1))} \\\\ {=>390625=5(n-1)} \\\\ {=>5^(8)=5^((n-1))}\end{array}`

Since base that is 5 is same on both sides, so exponent will be equal

=>8 = n – 1

=> n = 8 + 1 = 9

=> n = 9

Hence there are 9 terms in geometric series