Question

A 3.1 kg dog stands on an 18 kg flatboat and is 6.1 m from the shore. He walks 2.5 m on the boat toward shore and then stops. Assuming there is no friction between the boat and the water, find how far the dog is then from the shore? The dog moves leftward; the boat moves rightward; but does the center of mass of the boat + dog system move?)

Answer 1

The distance of dog from the shore is 3.97 m

Step-by-step explanation:

given,

mass of the dog = 3.1 Kg

mass of the flatboat = 18 Kg

Distance from the shore = 6.1 m

dog moves on boat = 2.5 m

dog moves leftward and boat moves rightward.

If it's a frictionless system with no initial velocity, the center of mass doesn't move. Conservation of momentum, which = 0 in this case.

When dog move toward the shore a reactive force will act on the boat.

`m_b x_b + m_d x_d = 0`

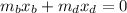
m_b i and m_d is mass of boat and mass of dog.

x_b and x_d is distance moved by the boat and the dog.

`x_b = (m_dx_d)/(m_b)`

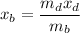
neglecting negative sign

x_b + x_d = 2.5

`(m_dx_d)/(m_b) + x_d = 2.5`

`x_d = (2.5)/(1+(m_d)/(m_b))`

`x_d = (2.5)/(1+(3.1)/(18))`

`x_d = (2.5)/(1.172)`

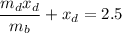
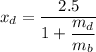
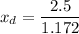
x_d = 2.133 m

The distance of dog from the shore is 6.1 – 2.133 = 3.97 m

The distance of dog from the shore is 3.97 m