Answer:
The velocity of the ball becomes half when the time period is doubled.
Step-by-step explanation:
Let
 be the time period of the ball,
be the time period of the ball,
 be radius and
be radius and
 be the velocity of the ball performing circular motion.
be the velocity of the ball performing circular motion.
Now, for a circular motion, the velocity is given as:
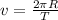
From the above relation, we can conclude that, velocity is inversely proportional to time period if the radius is constant.
This means that if time period is increased, velocity will decrease and vice-versa.
So, if time period is doubled, the velocity will reduce by half. This can be verified mathematically also given below.
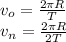
Divide
 by
by
 , we get
, we get
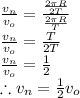
Here,
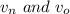 are the new and old velocities.
are the new and old velocities.
So, it can be concluded that if the time period is doubled, velocity is reduced by half.