The angle of elevation is 13.5 degrees approximately
Solution:
Given that , The length of a flagpole is 12cm
A student stands 50 m from the foot of the flagpole
Now, we have to observe that, above situation forms a right angle triangle with base 50 m and height of 12 m.
Then, we can apply,
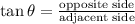
where
 is angle of elevation and opposite side is height and adjacent side becomes base
is angle of elevation and opposite side is height and adjacent side becomes base
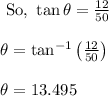
Hence, the angle of elevation is 13.5 degrees approximately.