Question

Which quadratic equation has roots - 1 + 4i and - 1 - 4i?. (1 point)

A. x^2+2x+2=0
B. 2x^2+x+17=0
C. x^2+x+2=0
D. 2x^2+x+2=0

Answer 1

Question:

Which quadratic equation has the roots -1+4i and -1-4i

A. X^2+2x+2=0

B. 2x^2+x+17=0

C. X^2+2x+17=0

D. 2x^2+x+2=0

Answer:

Option C

The quadratic equation that has roots -1 + 4i and -1 - 4i is
`x^(2)+2 x+17=0`

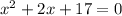
Solution:

Given, roots of a quadratic equation are (- 1 + 4i) and (- 1 – 4i)

We have to find the quadratic equation with above roots.

Now, as (-1 + 4i) and (-1 – 4i) are roots, x – (-1 + 4i) and x – (-1 – 4i) are factors of quadratic equation.

Then, equation will be product of its factors.

`(x-(-1+4 i)) *(x-(-1-4 i))=0`

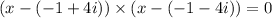
On multiplying each term with the terms in brackets we get,

`x^(2)+x+4 i x+x+1+4 i-4 i x-4 i-16 i^(2)`

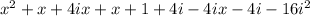
4ix and -4ix will cancel out each other.

Similarly 4i and -4i will cancel out each other

We know that
`i^2 = -1`

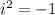
Hence we get,

`x^(2)+2 x+1+16=0`

`x^(2)+2 x+17=0`

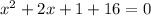
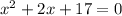
Thus
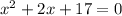`x^(2)+2 x+17=0` is the required quadratic equation