Question

Answer asap please

Which points are on the graph of f(x)=(1/3)^x
Select each correct answer
(0, 1)
(3, 27)
(-2,9)
(-1, -1/3)

Answer 1

(0,1) and (-2,9)

Explanation:

A point (x,y) lies on the graph of f(x) =
`((1)/(3) )^(x)` if it satisfies the condition y =
`((1)/(3) )^(x)`

(0,1):

x = 0 and y = 1.

This point satisfies the required condition as

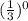`((1)/(3) )^(0)` = 1

Hence, this point is on the graph of f(x) =
`((1)/(3) )^(x)`

(3,27):

x = 3 and y = 27.

This point doesn't satisfy the required condition as

`((1)/(3) )^(3)` =
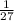`(1)/(27)` ≠ 27

Hence, this point is not on the graph of f(x) =
`((1)/(3) )^(x)`

(-2,9):

x = -2 and y = 9.

This point satisfies the required condition as

`((1)/(3) )^(-2)` =
`3^(2)` = 9

Hence, this point is on the graph of f(x) =
`((1)/(3) )^(x)`

(-1,
`-(1)/(3)`):

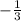x = -1 and y =
`-(1)/(3)`.

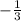This point satisfies the required condition as

y =
`((1)/(3) )^(-1)` =
`3^(1)` = 3 ≠
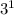`-(1)/(3)`

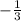
Hence, this point is not on the graph of f(x) =
`((1)/(3) )^(x)`