Question

A jar contains n nickels and d dimes. There are 18 coins in the jar, and the total value of the coins is $1.15. How many nickels and how many dimes are in the jar? (Hint: Nickels are worth $0.05 and dimes are worth $0.10.)

There are....... nickels and .....dimes in the jar.?

Answer 1

There are 13 nickels and 5 dimes in the jar.

Explanation:

Total number of coins = 18

Number of nickels =
`n`

Number of dimes =
`d`

Therefore
`n+d=18`

Total value of coins = $1.15

Value of
`n` nickels = $
`0.05n`

Values of
`d` dimes = $
`0.10d`

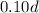
therefore
`0.05n+0.10d=1.15`

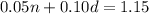
We have a system of equation to solve

(1)
`n+d=18`

(2)
`0.05n+0.10d=1.15`

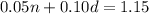
Multiplying equation (2) with
`-10`

`-0.5n-d=-11.5`

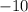
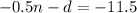
Now adding it to equation (1)

`n+d=18`

`-0.5n-d=-11.5`

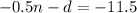
We get
`0.5n=6.5`

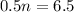
Dividing both sides by
`0.5`

`(0.5n)/(0.5)=(6.5)/(0.5)`

∴
`n=13`

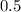
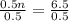
Plugging value of
`n` in equation (1).

`13+d=18`

Subtracting both sides by 13.

`13+d-13=18-13`

∴
`d=5`

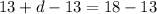
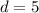
Therefore there are 13 nickels and 5 dimes in the jar.