Question

Calculus
The following curve passes through (3,1)
Using linear lineralization

Answer 1

Option 1.1

Explanation:

The linearization of a curve implies the use of calculus to find the local value for the derivative and approximating the function by the use of the formula

`F(x) \approx F(x_0) + F'(x_0)(x-x_0)`

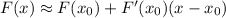
The function is given in such way that it's much easier to find the derivative by implicit differentiation than isolating any of the variables

`2x^2y+y=2x+13`

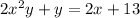
Differentiating with respect to x, we have

`4xy+2x^2y'+y'=2`

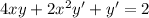
Computing y' in the given point (3,1) we have

4(3)(1)+2(9)y'+y'=2

`y'=(2-12)/(19)`

`y'=-(10)/(19)`

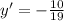
The function will be approximated with the expression

`F(x) = 1 -(10)/(19)(x-3)`

To find the approximate value for x=2.8

`F(2.8) = 1-(10)/(19)(-0.2)=1.1`

The correct value is the option 1.1