Question

Cari nilai sudut APB​

Answer 1

The measurement of ∠APB=80°

Explanation:

Given:

In quadrilateral ABCD ∠C=100° and ∠D=60° .

Now, let ∠PAB=
`x` and ∠PBA=
`y`

As, sum of all interior angles of a quadrilateral is 360°.

∠A+∠B+∠C+∠D=360°

⇒
`2x+2y+100+60=360`

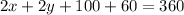
(as the line AP and BP bisect ∠A and ∠B respectively so, ∠A=2x and ∠B=2y)

⇒
`2x+2y+160=360`

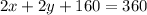
subtracting 160 on both sides

⇒
`2x+2y=200`

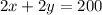
dividing by 2 on both the sides

⇒
`(2x)/(2) +(2y)/(2)=(200)/(2)`

⇒
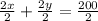
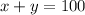`x+y=100` ........(1)

Now, in triangle PAB:

Sum of interior angles of triangle is 180°.

∠PAB+∠PBA+∠APB=180°

Let ∠APB be z.

⇒
`x+y+z=180`

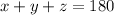
Putting the value from the above equation (1)

⇒
`100+z=180`

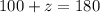
Subtracting 100 from both sides

⇒
`z=80`

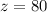
⇒ ∠APB=80°

Therefore, the measurement of ∠APB=80° .