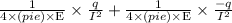Answer:
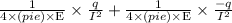
Step-by-step explanation:
As given point p is equidistant from both the charges
It must be in the middle of both the charges
Assuming all 3 points lie on the same line
Electric Field due a charge q at a point ,distance r away
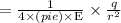
Where
- q is the charge
- r is the distance
-
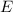 is the permittivity of medium
is the permittivity of medium
Let electric field due to charge q be F1 and -q be F2
I is the distance of P from q and also from charge -q
⇒
F1
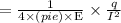
F2
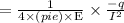
⇒
F1+F2=