Question

Is it ever possible that cos (A−B)=cos ⁡A−cos ⁡B? Why or why not?

Answer 1

The given equation is never possible i.e cos ( A - B ) ≠ cos A - cos B

Explanation:

Given as :

Is cos ( A - B ) = cos A - cos B

To check this possibility , Let us put the value of angle A and B on both side of equation

Now, Let A = 60° and B = 30°

From Left hand side equation

cos ( A - B ) = cos ( 60° - 30° )

Or, cos ( A - B ) = cos 30°

∴ cos ( A - B ) =
`(√(3) )/(2)`

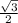
or, cos ( A - B ) = 0.866

From Right hand side equation

cos A - cos B = cos 60° - cos 30°

Or, cos A - cos B =
`(1)/(2)` -
`(√(3) )/(2)`

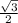
∴, cos A - cos B = 0.5 - 0.866

I.e cos A - cos B = - 0.366

So, Left hand side ≠ Right hand side

Since while equating the values of angle A and b in the given equation on both sides, we get that the value of both sides are not equal , Thus we can say that the given equation is not equal to each other .

Hence given equation is never possible i.e cos ( A - B ) ≠ cos A - cos B Answer