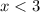Answer:
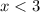
Explanation:

Solving the inequality to have solutions for

Subtracting 4 from both sides.
⇒
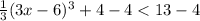
⇒
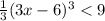
Multiplying 3 both sides to remove fraction.
⇒
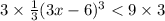
⇒
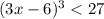
Taking cube root both sides to remove the cube.
⇒
![\sqrt[3]{(3x-6)^3}<\sqrt[3]{27}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/twhaib54lsrh276hgtq38yy5kwv9r01jho.png)
⇒
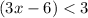 [ ∵
[ ∵
![\sqrt[3]{27} =3](https://img.qammunity.org/2020/formulas/mathematics/middle-school/1pyiij3cl7pntv1fmdf4ukwhjlajillnj1.png) ]
]
Adding 6 to both sides.
⇒
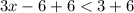
⇒
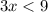
Dividing both sides by
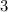
⇒
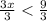
∴