Factor the following expression: 6x^5-11x^4-10x^3-54x^3+99x^2+90x

Question

Factor the following expression:

`6x^5-11x^4-10x^3-54x^3+99x^2+90x`

Answer 1

(3x+2)(2x-5)(x³ -9)

Explanation:

I like to use a graphing calculator to assist with factoring higher-degree polynomials. This polynomial has roots at -2/3, +5/2, and an irrational number near 2.08. The factors corresponding to the rational roots are (3x +2) and (2x -5).

Polynomial long division or synthetic division can be used to divide these out.

In each case, the divisor has a coefficient other than 1, so both dividend and divisor polynomials need to be divided by that coefficient before proceeding with synthetic division. (That is why there are fractions in the tableaux.)

The result is that the factorization in integers is ...

`6x^5-11x^4-10x^3-54x^2+99x+90=\bf{(3x+2)(2x-5)(x^3-9)}`

_____

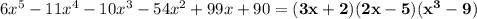
The irrational roots are the three cube roots of 9, two of which are complex.

_____

Any of several different algorithms can tell you that the real roots will lie in the interval [-6, 6] or smaller. The rational roots will be of the form ...

±(divisor of 90)/(divisor of 6)