Question

An area of a rectangle is represented by the function p(x)=3x^3+14x^2-23x+6. The width of the rectangle is represented as x + 6 . What is the expression for the length of the rectangle?

3x^2-4x+1
3x^2+4x-1
3x^2-4x-1
3x^2+4x+1

Answer 1

Answer:
`3x^(2)-4x+1`

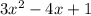
Explanation:

Let
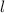`l` be the length of the rectangle.

Let
`b` be the breadth of the rectangle.

The area of the rectangle with length
`l` an breadth
`b` is given by
`l* b`

Given that
`b=x+6`

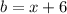
Given that area is
`3x^(3)+14x^(2)-23x+6`

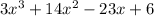
Option A:

`lb=(x+6)(3x^(2)-4x+1)=3x^(3)-4x^(2)+x+18x^(2)-24x+6=3x^(3)+14x^(2)-23x+6`

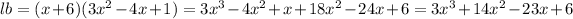
This is the area given.So,option A is correct.

Option B:

`lb=(x+6)(3x^(2)+4x-1)=3x^(3)+4x^(2)-x+18x^(2)+24x-6=3x^(3)+22x^(2)+23x-6`

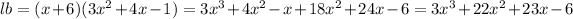
But this is not the area given.So,option B is wrong.

Option C:

`lb=(x+6)(3x^(2)-4x-1)=3x^(3)-4x^(2)-x+18x^(2)-24x-6=3x^(3)+14x^(2)-25x-6`

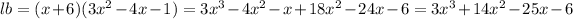
But this is not the area given.So,option C is wrong.

Option D:

`lb=(x+6)(3x^(2)+4x+1)=3x^(3)+4x^(2)-x+18x^(2)-24x-6=3x^(3)+14x^(2)-25x-6`

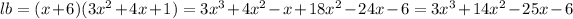
But this is not the area given.So,option D is wrong.