Question

In the coordinate plane, you plot the point $(2t + 3, -3t + 3)$ for every real number $t.$ For example, when $t=5$, we have $2t + 3 = 13$ and $-3t + 3 = -12$, so the point $(13,-12)$ is on the graph. Explain why the resulting graph is a line, and find an equation whose graph is this line.

SHOW YOUR WORK AN THOROUGHLY EXPLAIN WHY YOUR ANSWER IS YOUR ANSWER PLEASE!!!

Answer 1

The locus of the coordinates given is a straight line having equation 3x + 2y = 15.

Explanation:

Let at any particular value of t, the coordinates of the point are (h,k).

So, h = 2t + 3

⇒ 2t = h - 3

⇒
`t = (h - 3)/(2)`

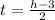
Again, k = - 3t + 3

⇒ 3t = 3 - k

⇒
`t = (3 - k)/(3)`

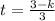
Therefore, eliminating t we get a relation between h and k.

Hence,
`(h - 3)/(2) =  (3 - k)/(3)`

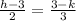
⇒ 3h - 9 = 6 - 2k

⇒ 3h + 2k = 15

Therefore, converting in to current coordinates we get the locus of the point (h,k) as 3x + 2y = 15, which is a straight line.

For this reason, the resulting graph is a line and its equation is 3x + 2y = 15. (Answer)