Question

Equation of a line with an slope of 1/2 that contains (-4, 7)

Answer 1

Equation of a line with an slope of 1/2 that contains (-4, 7) is
`y=(1)/(2) x+9`

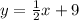
Solution:

We have been given a point and slope of an equation and have been asked to write it in an equation. The two forms of writing a point and slope in equation are point slope form and standard form.

The standard form of a line is in the form Ax + By = C where A is a positive integer, and B, and C are integers. The standard form of a line is just another way of writing the equation of a line.

To write in standard form we will first write it in point slope form and then rearrange it into a standard from.

The formula for point slope form:

`y-y_(1)=m\left(x-x_(1)\right)`

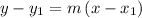
where "m" is the slope of line

Given that "m" =
`(1)/(2)` and
`(x_1, y_1) = (-4, 7)`

`\begin{array}{l}{y-7=(1)/(2)(x-(-4))} \\\\ {y-7=(1)/(2)(x+4)} \\\\ {y-7=(1)/(2) x+2} \\\\ {y=(1)/(2) x+9}\end{array}`

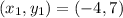
Now, let us convert this equation to standard form

0.5x + 9 = y

0.5x - y = -9

Thus we have found out equation of line in point slope and standard form