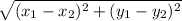Question

What is the length of the mid segment of this trapezoid a(-11,3), b(0,3), d(-8,-2), and c(-1,-2)

? Units

Answer 1

9 units.

Explanation:

Let ab and cd are the parallel sides of the given parallelogram.

Hence
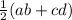`(1)/(2) (ab + cd)` is the mid segment of this trapezoid.

Now, coordinates of a, b, c and d are respectively (-11,3), (0,3), (-8,-2), and (-1,-2).

So, the length of ab =
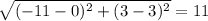`\sqrt{(-11 - 0)^(2) + (3 - 3)^(2)} = 11` units

And the length of cd =
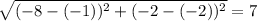`\sqrt{(-8 - (- 1))^(2) + (- 2 - ( - 2))^(2)  } = 7` units

Therefore, the mid segment of this trapezoid is
`(1)/(2) (11 + 7) = 9` units. (Answer)

The length of a straight line connecting two points (
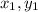`x_(1), y_(1)`) and (
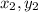`x_(2), y_(2)`) is equal to

`\sqrt{(x_(1) - x_(2))^(2) + (y_(1) - y_(2))^(2) }`