Question

Consider U = x.

Which is an empty set?
O x e U and x has a negative cube root
O {x\X EU and x has a negative square root}
O x
O x

Answer 1

{x\ x e U and x has a negative square root} is an empty set.

Explanation:

If x e U, x is a negative real number, and they don't have a square root (they don't have even roots). Their square roots are complex numbers, not real ones.

Answer 2

Option B.

Explanation:

Consider,

`U=\{x|x\text{ is a negative real number }\}`

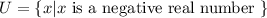
We need to find the empty set from the given options.

In option A,

Let
`S_1=\{x|x\in U\text{ and }x \text{ has a negative cube root}\}`

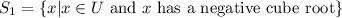
Since x has a negative cube root, it means x is a negative real number. So, this set is not an empty set.

In option B,

Let
`S_2=\{x|x\in U\text{ and }x \text{ has a negative square root}\}`

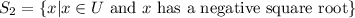
Since x has a negative square root, it means x is a positive real number because square root of a negative number is an imaginary number. So, this set is an empty set.

In option C,

Let
`S_3=\{x|x\in U\text{ and }x \text{ is equal to the product of a positive number and -1}\}`

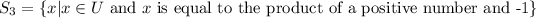
Since x is equal to the product of a positive number and -1, it means x is a negative real number. So, this set is not an empty set.

In option D,

Let
`S_4=\{x|x\in U\text{ and }x \text{ is equal to the sum of one negative and one positive number}\}`

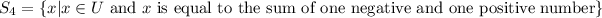
Since x is equal to the sum of one negative and one positive number, it means x can be a negative real number or positive real number. So, this set is not an empty set.

Hence, option B is correct.