Question

For what values of K does x^2+kx+4=0 have two equal real roots?

k>4
k=+4
K<-4
k=-4

Answer 1

For k= +4, the polynomial has two equal roots.

For k = -4, the polynomial has two equal roots.

Explanation:

Here, the given expression is :
`x^(2)   + kx + 4 = 0`

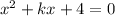
(1) Now, let us assume the value of k = +4

So, the expression is
`x^(2)   + 4x + 4 = 0`

Simplifying the given by splitting,

`x^(2)   + 4x + 4 = 0  \implies x^(2)   + 2 x + 2x + 4\\\implies x(x+2) +2(x+2)  =0\\or, (x+2)(x+2) = 0`

`x = -2,  x= -2`

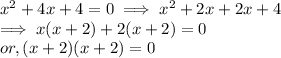
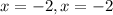
Hence, for k= +4, the polynomial has two equal roots.

Now, let us assume the value of k = -4

So, the expression is
`x^(2)   - 4x + 4 = 0`

Simplifying the given by splitting,

`x^(2)   - 4x + 4 = 0  \implies x^(2)   - 2 x - 2x + 4\\\implies x(x-2) -2(x-2)  =0\\or, (x-2)(x-2) = 0`

`x = 2,  x= 2`

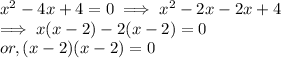
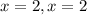
Hence, for k = -4, the polynomial has two equal roots.

(3) Let us assume the value of k < -4

This gives us NO FIXED VALUE for k.

So, the expression is
`x^(2)   + 4x + 4 = 0` can not be solved.

(4) let us assume the value of k > 4

This gives us NO FIXED VALUE for k.

So, the expression is
`x^(2)   + 4x + 4 = 0` can not be solved.

Hence, for k =+4, and k = -4 the polynomial has two equal roots.