Question

A 50 kg rocket generates 990 N of thrust. What will be its acceleration if it is launched straight up?

Answer 1

The acceleration of the rocket is 10 m/s².

Step-by-step explanation:

Let the acceleration of the rocket be
`a` m/s².

Given:

Mass of the rocket is,
`m=50\ kg`

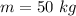
Thrust force acting upward is,
`F_(th)=990\ N`

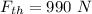
Acceleration due to gravity is,
`g=9.8\ m/s^2`

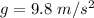
Now, force acting in the downward direction is due to the weight of the rocket and is given as:

`W=mg=50* 9.8=490\ N`

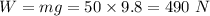
Now, net force acting on the rocket in upward direction is given as:

`F_(net)=F_(th)-W\\F_(net)=990-490=500\ N`

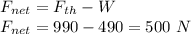
Therefore, from Newton's second law, net force acting on the rocket is equal to the product of mass and acceleration.

`F_(net)=ma\\500=50a\\a=(500)/(50)=10\ m/s^2`

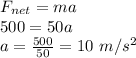
Therefore, the acceleration of the rocket is 10 m/s².