Question

Two pipes are connected to the same tank. When working together, they can fill in 2hrs. The larger pipe, working alone, can fill the tank in 3 hrs less time than the smaller one. How long would the smaller one take, working alone, to fill the tank?

Answer 1

The smaller pipe can fill the tank in 6 hours alone.

Explanation:

Let us assume that the smaller pipe can fill the tank alone in x hours and the larger pipe fills it in (x - 3) hours.

Therefore, the smaller pipe in 1 hour can fill
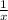`(1)/(x)` part of the tank.

Again the larger pipe in 1 hour can fill
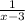`(1)/(x - 3)` part of the tank.

So, if both the pipes are open then, in 1 hour they can fill (
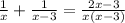`(1)/(x) + (1)/(x - 3) = (2x - 3)/(x(x - 3))` part of the tank.

Therefore, they can fill the full tank in
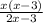`(x(x - 3))/(2x - 3)` hours.

As per given condition, we can write

`(x(x - 3))/(2x - 3) = 2`

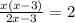
⇒ x² - 3x = 4x - 6

⇒ x² - 7x + 6 = 0

⇒ (x - 6)(x - 1) = 0

⇒x = 6 or x = 1

But x can not be less than 2 hours.

So, x = 6 hours.

Therefore, the smaller pipe can fill the tank in 6 hours alone. (Answer)