Question

A merchant bought some shirts for $120. The next day the price charged for each shirt was reduced by $1. The merchant calculated that, at the sale price, he could have bought 10 more shirts for $120. How many shirts did he buy originally?

Answer 1

The merchant buys 30 shirts originally.

Explanation:

Let us assume that the merchant bought x numbers of shirts in $120.

So, the cost for each shirt is $
`(120)/(x)`.

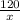Now, if the cost for each shirt is reduced by 1$, then he would have bought 10 shirts more i.e. (x + 10) shirts in $120.

So, we can write the following equation as

`((120)/(x) - 1)(x + 10) = 120`

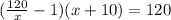
⇒(120 - x)(x + 10) = 120x

⇒ 120x - 10x + 1200 - x² = 120x

⇒ x² +10x - 1200 = 0

⇒ x² + 40x - 30x - 1200 = 0

⇒(x + 40)(x - 30) = 0

⇒ x = - 40 or x = 30

But x can not be negative.

Hence, the merchant buys 30 shirts originally. (Answer)