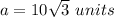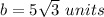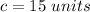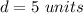Question

Find the value of each variable help fast

Answer 1

`a=10√(3)\ units`,
`b=5√(3)\ units`,
`c=15\ units`,
`d=5\ units`

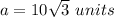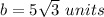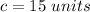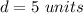
Explanation:

see the attached figure with letters to better understand the problem

step 1

Find the value of b

In the right triangle BCD

`sin(60\°)=(b)/(10)`

`b=sin(60\°)(10)`

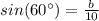
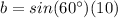
Remember that

`sin(60\°)=(√(3))/(2)`

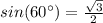
so

`b=(√(3))/(2)(10)`

`b=5√(3)\ units`

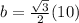
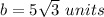
step 2

Find the value of d

In the right triangle BCD

`cos(60\°)=(d)/(10)`

`d=cos(60\°)(10)`

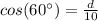
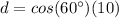
Remember that

`cos(60\°)=(1)/(2)`

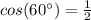
so

`d=(1)/(2)(10)`

`d=5\ units`

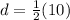
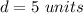
step 3

Find the value of a

In the right triangle ABD

`sin(30\°)=(b)/(a)`

`a=(b)/(sin(30\°))`

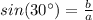
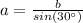
Remember that

`sin(30\°)=(1)/(2)`

`b=5√(3)\ units`

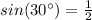
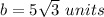
so

`a=(5√(3))/((1/2))`

`a=10√(3)\ units`

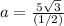
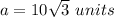
step 4

Find the value of c

In the right triangle ABD

`cos(30\°)=(c)/(a)`

`c=(a)cos(30\°)`

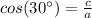
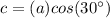
Remember that

`cos(30\°)=(√(3))/(2)`

`a=10√(3)\ units`

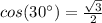
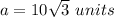
substitute

`c=(10√(3))(√(3))/(2)`

`c=15\ units`

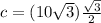
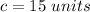
therefore

`a=10√(3)\ units`

`b=5√(3)\ units`

`c=15\ units`

`d=5\ units`