Question

A meter stick balances horizontally on a knife-edge at the 50.0 cm mark. With two 4.79 g coins stacked over the 28.8 cm mark, the stick is found to balance at the 38.4 cm mark. What is the mass of the meter stick?

Answer 1

To solve the exercise, the key concept to be addressed is the Mass Center.

The center of mass of an object is measured as,

`X_(cm) = (\sum m_ix_i)/(\sum m_i)`

`X_(cm) = (m_1x_1+m_2x_2+m_3x_3)/(m_1+m_2+m_3)`

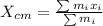
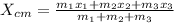
Our values are given by,

`x_1 = 50cm`

`m_1 = ?`

`x_2 =28.8cm`

`m_2 = 4.79g`

`x_3 = 28.8cm`

`m_3 = 4.79g`

`X_(cm) = 38.4cm`

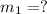
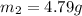
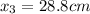
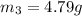
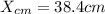
Replacing the values in our previous equation we have,

`X_(cm) = (m_1x_1+m_2x_2+m_3x_3)/(m_1+m_2+m_3)`

`38.4 = (m_1(50)+2(28.8*4.79))/(m_1+2*4.79)`

`38.4(m_1+2*4.79)= m_1(50)+2(28.8*4.79)`

`38.4m_1 +367.872 = 50m_1+275.904`

`11.6m_1 = 91.968`

`m_1 = 7.928g`

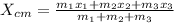
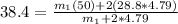
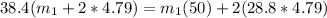
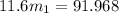
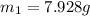
Therefore the mass of the meter stick is 7.928g