Question

A rogue black hole with a mass 12 times the mass of the sun drifts into the solar system on a collision course with earth. How far is the black hole from the center of the earth when objects on the earth’s surface begin to lift into the air and ""fall"" up into the black hole? Give your answer as a multiple of the earth’s radius.

Answer 1

Distance of blackhole from center of earth 2000 Re

Step-by-step explanation:

we have mass of earth
`= Me = 5.972 * 10^(24) kg`

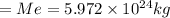
Mass of black hole
`Mb = 12 * M_(sun) = 12 * 1.989 * 10^(30) kg = 23.868 * 10^(30) kg`

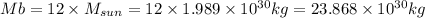
Object start to lift in air when net force on them becomes zero

`( G Mb m)/(x^2) = (GM_(sun) m)/(Re^2)`

`(MB)/(x^2) = (M_E)/(R_E^2)`

`x = \sqrt{(Mb)/(M_E)} R_E`

`x = \sqrt{(23.868 * 10^(30))/(5.972 * 10^(24))} R_E`

`x = 1.99 * 10^(3) Re`

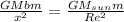
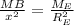
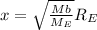
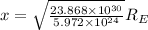
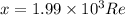
x = 1999.16 Re

So, distance of blackhole from center of earth will be = x+ Re

= 1999.16 Re + Re = 2000.16 Re